介绍

树

–》二叉树

–》–》完全二叉树

–》–》–》满二叉树

完全二叉树高度：h = logN + 1

满二叉树高度：h = log(N+1)

OJ

1.单值二叉树

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回 true；否则返回 false。

示例 1：

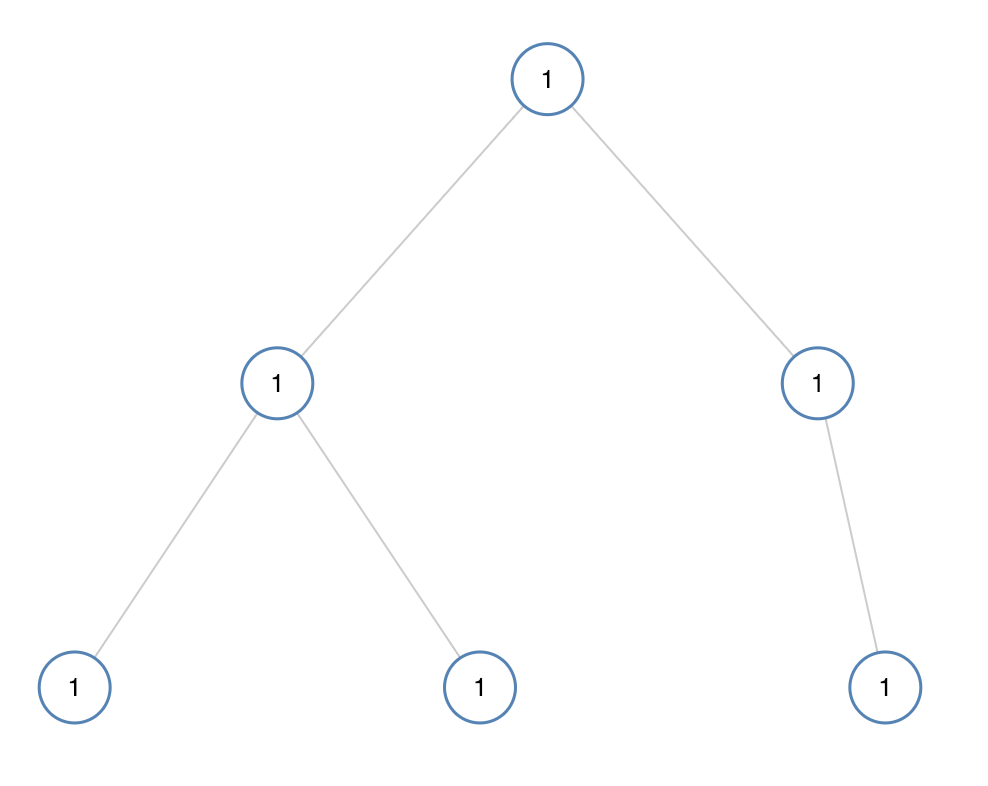
输入：[1,1,1,1,1,null,1]
输出：true

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isUnivalTree(struct TreeNode* root) {
    
    if(root == NULL)
    {
        return true;
    }

    if(root->left&& root->val != root->left->val)
        return false;
    if(root->right&& root->val != root->right->val)
        return false;

    return isUnivalTree(root->left)&&isUnivalTree(root->right);
}

2.二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：3

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
int maxDepth(struct TreeNode* root) {
    
    if(root == NULL)
    {
        return 0;
    }

    int left = maxDepth(root->left);
    int right = maxDepth(root->right);
    return left>right? left+1:right+1;

}

3.翻转二叉树

给定一棵二叉树的根节点 root，请左右翻转这棵二叉树，并返回其根节点。

示例 1：

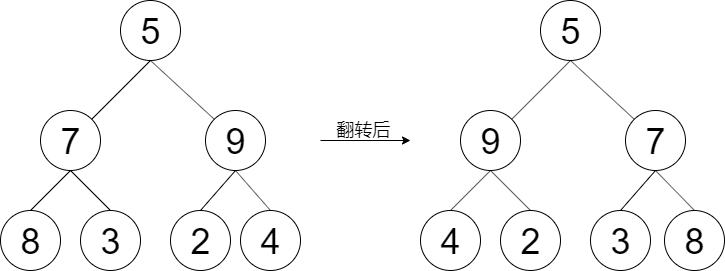
输入：root = [5,7,9,8,3,2,4]
输出：[5,9,7,4,2,3,8]

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
// struct TreeNode* flipTree(struct TreeNode* root) {
    
//     if(root == NULL)
//     {
//         return NULL;
//     }

//     struct TreeNode* left = root->left;
//     root->left = root->right;
//     root->right = left;

//     flipTree(root->left);
//     flipTree(root->right);
//     return root;

// }
//法二
struct TreeNode* flipTree(struct TreeNode* root) {
    
    if(root == NULL)
    {
        return NULL;
    }

    struct TreeNode* left = flipTree(root->left);
    root->left = flipTree(root->right);
    root->right = left;
    
    return root;



}

4.相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

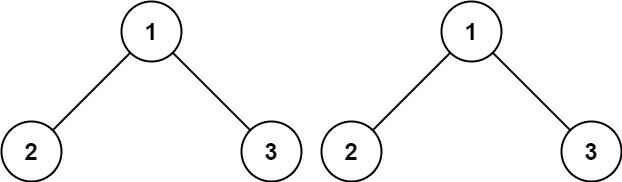
输入：p = [1,2,3], q = [1,2,3]
输出：true

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    
    //结束条件
    if(p==NULL&&q==NULL)
        return true;

    //结构上
    if(p==NULL&&q!=NULL)
        return false;
    if(p!=NULL&&q==NULL)
        return false;

    if(p->val!=q->val)
        return false;
    
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);

}

5.对称二叉树

给你一个二叉树的根节点 root ，检查它是否轴对称。

示例 1：

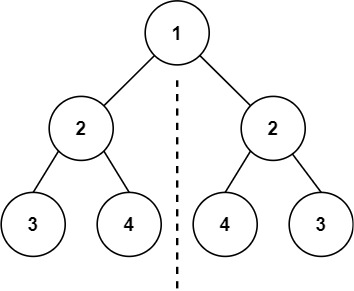
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

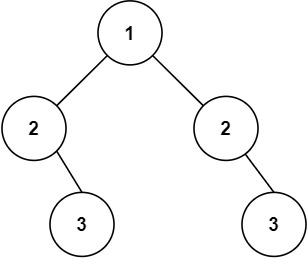
输入：root = [1,2,2,null,3,null,3]
输出：false

算法思路：从第一层开始判断左右子树的结构是否对称，然后以第二层左右结点为根，判断其两个子树左右结构上是否相同，结构相同判断结点值是否相同，依次往下判断第三第四层，当左右结点都为空表示结束。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
typedef struct TreeNode Node;
bool _isSymmetric(Node* root1,Node* root2)
{
    if(root1==NULL&&root2==NULL)
        return true;
    
    //结构上
    if(root1!=NULL&&root2==NULL)
        return false;
    if(root1==NULL&&root2!=NULL)
        return false;
    //结点值上
    if(root1->val != root2->val)
        return false;

    if(_isSymmetric(root1->left,root2->right)&&_isSymmetric(root1->right,root2->left))
        return true;

    return false;

}


bool isSymmetric(struct TreeNode* root) {
    
    return _isSymmetric(root->left,root->right);

}

6.另一个树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。

二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

示例 1：

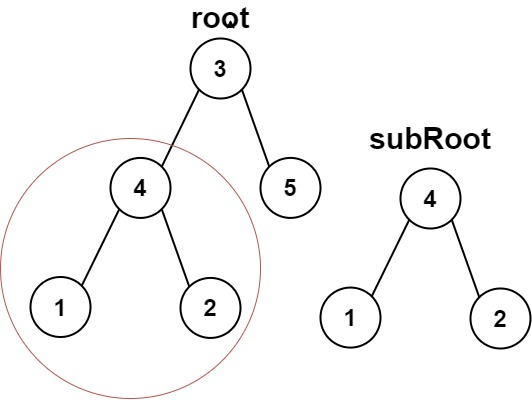
输入：root = [3,4,5,1,2], subRoot = [4,1,2]
输出：true

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
//相同的树
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    
    //结束条件
    if(p==NULL&&q==NULL)
        return true;

    //结构上
    if(p==NULL&&q!=NULL)
        return false;
    if(p!=NULL&&q==NULL)
        return false;

    if(p->val!=q->val)
        return false;
    
    return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);

}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
    
    if(root == NULL)
        return false;

    if(isSameTree(root,subRoot))
        return true;
	
    return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);

}

7.平衡二叉树

给定一个二叉树，判断它是否是平衡二叉树

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：true

算法思路：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */

// int TreeDepth(struct TreeNode* root)
// {
//     if(root==NULL)
//         return 0;
//     int left = TreeDepth(root->left);
//     int right = TreeDepth(root->right);
//     return left>right?left+1:right+1;
// }
//最好是O(N),最坏是O(N*N)  重复计算子树的高度
// bool isBalanced(struct TreeNode* root) {
    
//     if(root == NULL)
//         return true;
    
//     int leftDepth = TreeDepth(root->left);
//     int rightDepth = TreeDepth(root->right);

//     if(abs(leftDepth-rightDepth)>1)
//         return false;
    
//     return isBalanced(root->left)&&isBalanced(root->right);

// }
//法二：要求优化到最坏是O(N)
//后序，判断的同时带高度
bool _isBalanced(struct TreeNode* root,int* pDepth)
{
    if(root == NULL)
    {
        *pDepth = 0;
        return true;
    }   

    int leftDepth = 0;
    if(_isBalanced(root->left,&leftDepth) == false)
        return false;
    int rightDepth = 0;
    if(_isBalanced(root->right,&rightDepth) == false)
        return false;

    if(abs(leftDepth-rightDepth)>1)
        return false;
    
    *pDepth = leftDepth>rightDepth?leftDepth+1:rightDepth+1;
    return true;
}

bool isBalanced(struct TreeNode* root) {

    int depth = 0;
    return _isBalanced(root,&depth);

}

8.给你一个字符串构建二叉树

typedef struct BinaryTreeNode
{
	BTDataType _data;
	struct BinaryTreeNode* _left;
	struct BinaryTreeNode* _right;
}BTNode;


BTNode* CreateTree(char* str, int* pi)
{
	if (str[*pi] == NULL)
	{
		(*pi)++;
		return NULL;
	}
	else
	{
		BTNode* root = (BTNode*)malloc(sizeof(BTNode));
		root->_data = str[*pi];
		(*pi)++;
		root->_left = CreateTree(str,pi);
		root->_right = CreateTree(str,pi);
		return root;

	}
}


int main()
{
	
	
	char str[100];//ab##c##
	scanf("%s", str);

	int i = 0;
	BTNode* root = CreateTree(str, &i);

	return 0;
}

9.二叉树第K层结点的个数

//分治思想，大问题化为若干类似小问题
int BTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	//k=1时侯 才是第k层
	if (k == 1)
	{
		return 1;
	}

	return BTreeLevelKSize(root->_left, k - 1) 
		+ BTreeLevelKSize(root->_right, k - 1);
}

10.二叉树简单操作

//二叉树中查找x结点
BTNode* BTreeFind(BTNode* root, BTDataType x);
//二叉树销毁
void BTDestory(BTNode* root);
//二叉树层序遍历
void BTLevelOrder(BTNode* root);

//二叉树查找值为x的结点
BTNode* BTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	BTNode* node = BTreeFind(root->_left, x);
	if (node)
	{
		return node;
	}
	BTNode* node = BTreeFind(root->_right, x);
	if (node)
	{
		return node;
	}
	return NULL;;
}

void BTDestory(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	BTDestory(root->_left);
	BTDestory(root->_right);
	free(root);
	root = NULL;
}
//二叉树层次遍历
void BTLevelOrder(BTNode* root)
{
	Queue q;
	InitQueue(&q);


	if (root == NULL) {
		return;
	}
	QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%c ", front->_data);

		if (front->_left)
		{
			QueuePush(&q, front->_left);
		}
		if (front->_right)
		{
			QueuePush(&q, front->_right);
		}
	}

	QueueDestory(&q);
	printf("\n");
}

11.判断二叉树是否是完全二叉树

算法思路：

//判断是否是完全二叉树 在层次遍历基础上，当出现NULL结点时，判断队列是否有不为NULL结点存在
int BTComplete(BTNode* root)
{
	Queue q;
	InitQueue(&q);


	if (root == NULL) {
		return 1;
	}
	QueuePush(&q, root);

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		//printf("%c ", front->_data);
		if (front == NULL)
		{
			break;
		}

		QueuePush(&q, front->_left);
		QueuePush(&q, front->_right);

	}
	//判断队列是否有非空结点存在
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestory(&q);
			return 0;
		}
			
	}

	QueueDestory(&q);
	printf("\n");
	return 1;
}

堆

OJ

1.最小的k个数

设计一个算法，找出数组中最小的k个数。以任意顺序返回这k个数均可。

示例：

输入： arr = [1,3,5,7,2,4,6,8], k = 4
输出： [1,2,3,4]

算法思路：通过堆的特性，大根堆中父亲结点都是大于左右孩子结点，那么先选取数组中前K个元素建立拥有K个结点的大根堆，然后依次遍历剩下（N-K）个元素，通过与大根堆顶元素比较进行向下调整，如果该元素大于堆顶元素肯定不是要求K个数中之一（舍弃），如果该元素小于堆顶元素，把该元素赋值给堆顶元素，然后进行向下调整为大根堆，依次往下遍历数组，直到最后，那么此时堆中的K个结点即为所求最小K个数。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
 //堆排序 要实现递增建大根堆，实现递减建小根堆

//TopK 建拥有K个元素的堆， 找最小k个建大根堆，找最大k个建小根堆
int* smallestK(int* arr, int arrSize, int k, int* returnSize) {
    
    //
    *returnSize = k;

    //开辟k个大小的数组
    int* retArr = (int*)malloc(sizeof(int)*k); 

    if(k<1)
        return retArr;
    
    for(int i = 0;i<k;i++)
    {
        retArr[i] = arr[i];
    }

    void AdjustDown(int* a,int n,int root)
    {
        int parent = root;
        int child = parent*2+1;
        
        while(child<n)
        {
            //找出最大的孩子
            if(child+1<n && a[child]<a[child+1])
            {
                child++;
            }

            if(a[child]>a[parent])
            {   //交换父子，大的为父
                int tmp =  a[child];
                a[child] = a[parent];
                a[parent] = tmp;

                //继续向下调整
                parent = child;
                child = parent*2+1;
            }
            else
            {
                break;
            }
        }

    }
    //1.retArr建大根堆        根也要调整i>=0;
    //初始从第一个非叶结点开始向下调整，左右孩子小于父亲结点
    for(int i = (k-1-1)/2;i>=0;i--)
    {
        AdjustDown(retArr,k,i);
    }
    
    //2.遍历数组arr的元素与K堆顶进行比较(retArr[0]) 
    //比堆顶小的元素做向下调整
    for(int j = k;j<arrSize;j++)
    {
        if(arr[j]<retArr[0])
        {
            retArr[0] = arr[j];
            AdjustDown(retArr,k,0);
        }
    }

    return retArr;

}

数据结构>二叉树>堆

二叉树，堆

介绍

树

OJ

堆

OJ

CATALOG

FEATURED TAGS

FRIENDS